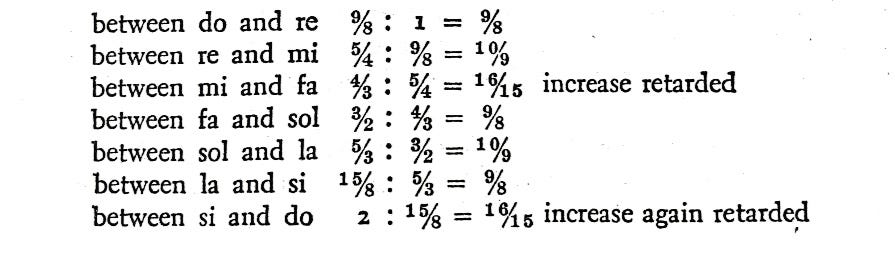This is the twenty fourth of our weekly readings in Fragments Reading Club from P.D. Ouspensky’s In Search of the Miraculous, where we are gradually working our way through the whole book. Please post comments and questions.
See this link for the beginning of the book.
(If you are a subscriber to The Journal of Gurdjieff Studies, you can opt in or out of receiving emails from the Fragments Reading Club category.)
The seven tone scale. The law of "intervals." Necessity for additional shocks. What occurs in the absence of additional shocks.
"The seven-tone scale is the formula of a cosmic law which was worked out by ancient schools and applied to music. At the same time, how-
125
ever, if we study the manifestations of the law of octaves in vibrations of other kinds we shall see that the laws are everywhere the same, and that light, heat, chemical, magnetic, and other vibrations are subject to the same laws as sound vibrations. For instance, the light scale is known to physics; in chemistry the periodic system of the elements is without doubt closely connected with the principle of octaves although this connection is still not fully clear to science.
"A study of the structure of the seven-tone musical scale gives a very good foundation for understanding the cosmic law of octaves.
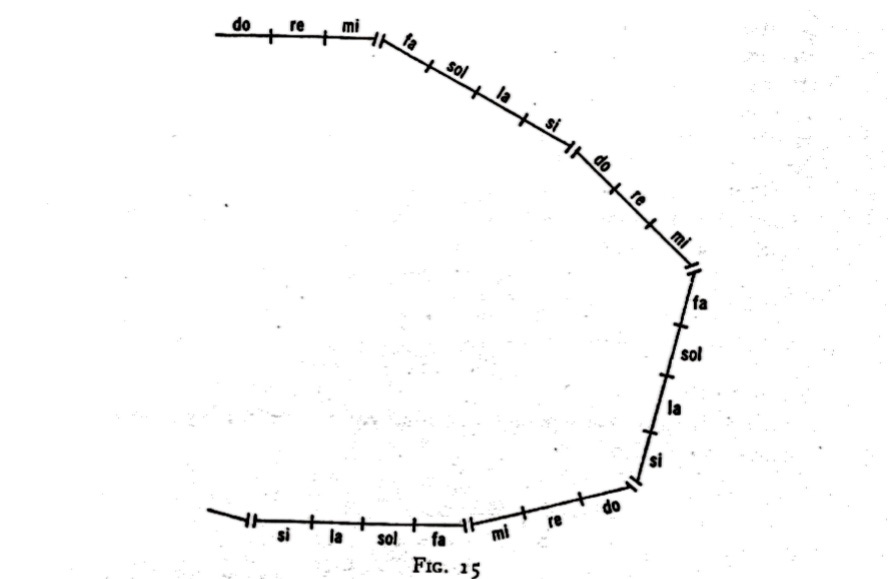
"Let us again take the ascending octave, that is, the octave in which the frequency of vibrations increases. Let us suppose that this octave begins with one thousand vibrations a second. Let us designate these thousand vibrations by the note do. Vibrations are growing, that is, their frequency is increasing. At the point where they reach two thousand vibrations a second there will be a second do, that is, the do of the next octave.
"The period between one do and the next, that is, an octave, is divided into seven unequal parts because the frequency of vibrations does not increase uniformly.
"The ratio of the pitch of the notes, or of the frequency of vibrations will be as follows:
"If we take do as 1 then re will be 9/8, mi 5/4, fa 4/3, sol 3/2, la 5/3, si 15/8, and do 2.
"The differences in the acceleration or increase in the notes or the difference in tone will be as follows:
126
"The differences in the notes or the differences in the pitch of the notes are called intervals. We see that there are three kinds of intervals in the octave: 9/8, 10/9, and 16/15, which in whole numbers correspond to 405, 400, and 384. The smallest interval 16/15 occurs between mi and fa and between si and do. These are precisely the places of retardation in the octave.
"In relation to the musical (seven-tone) scale it is generally considered (theoretically) that there are two semitones between each two notes, with the exception of the intervals mi-fa and si-do, which have only one semitone and in which one semitone is regarded as being left out.
"In this manner twenty notes are obtained, eight of which are fundamental:
do, re, mi, fa, sol, la, si, do
and twelve intermediate: two between each of the following two notes:
do-re
re-mi
fa-sol
sol-la
la-si
and one between each of the following two notes:
mi-fa
si-do
"But in practice, that is, in music, instead of twelve intermediate semitones only five are taken, that is one semitone between:
do-re
re-mi
fa-sol
sol-la
la-si
"Between mi and fa and between si and do the semitone is not taken at all.
"In this way the structure of the musical seven-tone scale gives a scheme of the cosmic law of 'intervals,' or absent semitones. In this respect when octaves are spoken of in a 'cosmic' or a 'mechanical' sense, only those intervals between mi-fa and si-do are called 'intervals'
"If we grasp its full meaning the law of octaves gives us an entirely new explanation of the whole of life, of the progress and development of phe-
127
nomena on all planes of the universe observed by us. This law explains why there are no straight lines in nature and also why we can neither think nor do, why everything with us is thought, why everything happens with us and happens usually in a way opposed to what we want or expect. All this is the clear and direct effect of the 'intervals,' or retardations in the development of vibrations.
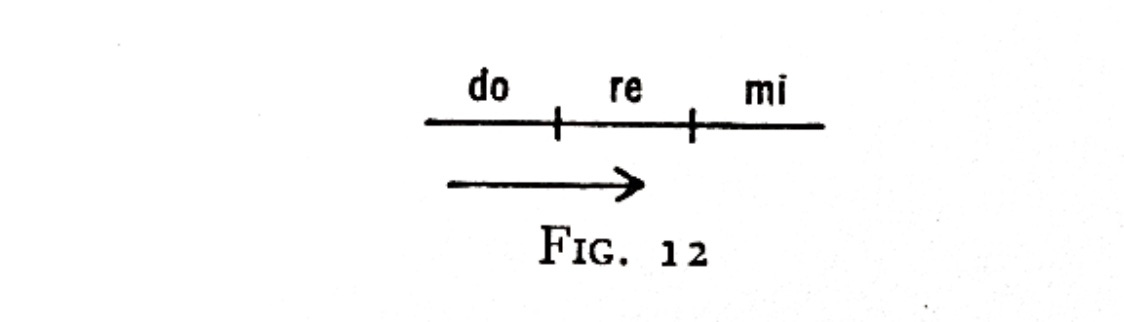
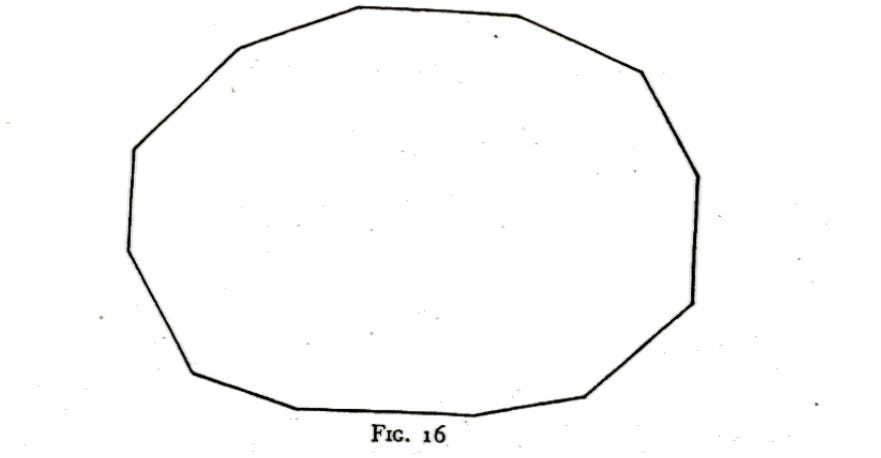
"What precisely does happen at the moment of the retardation of vibrations? A deviation from the original direction takes place. The octave begins in the direction shown by the arrow:
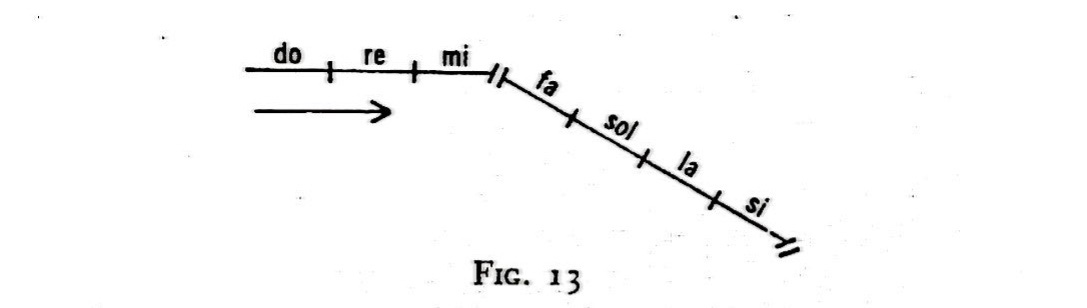
"But a deviation takes place between mi and fa; the line begun at do changes its direction
and through fa, sol, la, and si it descends at an angle to its original direction, shown by the first three notes. Between si and do the second 'interval' occurs—a fresh deviation, a further change of direction.
"The next octave gives an even more marked deviation, the one following that a deviation that is more marked still, so that the line of octaves may at last turn completely round and proceed in a direction opposite to the original direction.
128
"In developing further, the line of octaves or the line of development of vibrations may return to the original direction, in other words, make a complete circle.
"This law shows why straight lines never occur in our activities, why, having begun to do one thing, we in fact constantly do something entirely
129
different, often the opposite of the first, although we do not notice this and continue to think that we are doing the same thing that we began to do.
"All this and many other things can only be explained with the help of the law of octaves together with an understanding of the role and significance of 'intervals' which cause the line of the development of force constantly to change, to go in a broken line, to turn round, to become its 'own opposite' and so on.
"Such a course of things, that is, a change of direction, we can observe in everything. After a certain period of energetic activity or strong emotion or a right understanding a reaction comes, work becomes tedious and tiring; moments of fatigue and indifference enter into feeling; instead of right thinking a search for compromises begins; suppression, evasion of difficult problems. But the line continues to develop though now not in the same direction as at the beginning. Work becomes mechanical, feeling becomes weaker and weaker, descends to the level of the common events of the day; thought becomes dogmatic, literal. Everything proceeds in this way for a certain time, then again there is reaction, again a stop, again a deviation. The development of the force may continue but the work which was begun with great zeal and enthusiasm has become an obligatory and useless formality; a number of entirely foreign elements have entered into feeling—considering, vexation, irritation, hostility; thought goes round in a circle, repeating what was known before, and the way out which had been found becomes more and more lost.
"The same thing happens in all spheres of human activity. In literature, science, art, philosophy, religion, in individual and above all in social and political life, we can observe how the line of the development of forces deviates from its original direction and goes, after a certain time, in a diametrically opposite direction, still preserving its former name. A study of history from this point of view shows the most astonishing facts which mechanical humanity is far from desiring to notice. Perhaps the most interesting examples of such change of direction in the line of the development of forces can be found in the history of religion, particularly in the history of Christianity if it is studied dispassionately. Think how many turns the line of development of forces must have taken to come from the Gospel preaching of love to the Inquisition; or to go from the ascetics of the early centuries studying esoteric Christianity to the scholastics who calculated how many angels could be placed on the point of a needle.
"The law of octaves explains many phenomena in our lives which are incomprehensible.
"First is the principle of the deviation of forces.
"Second is the fact that nothing in the world stays in the same place, or remains what it was, everything moves, everything is going somewhere,
130
is changing, and inevitably either develops or goes down, weakens or degenerates, that is to say, it moves along either an ascending or a descending line of octaves.
"And third, that in the actual development itself of both ascending and descending octaves, fluctuations, rises and falls are constantly taking place.